常见的优化算法

发布时间：2024-05-26 10:19 浏览次数：次作者：佚名

前言

深度学习和普通的机器学习任务一样，需要模型(model)，数据集(dataset)，以及优化算法(optimizer)。在时下流行的Tensorflow, PyTorch中，优化算法仅仅是几行简单的代码:

import torch
import torch.optim as optim
'''
model=MyModel()
dataset=MyDataset()
'''
optimizer = optim.SGD(net.parameters(), lr = LR, momentum = 0.9, weight_decay = 5e-4)

事实上，像我当时直接结果导向地接触深度学习，还没能真正了解这些优化算法背后的原理，只知道它们存在的目的是优化自己的模型参数。后来在Cal上了Levine大大的CS282A以及准备秋招的过程中，才慢慢了解了这些优化算法背后的数学原理，也算是对模型参数的优化过程有一个浅薄的认知。当然，这其中涉及到的优化算法也仅仅是优化理论中的冰山一角，本人也还在刻苦学习中hhhh。

SGD是最为基础的优化算法，它的原理简单易懂，后续的各个优化算法几乎也都是按照它的数学公式为模板改进而来。

定义我们要优化的模型参数为 $w$ ,优化函数为 $f(w)$ 。在迭代轮数为 $t$ 时，优化 $w$ 的过程为

计算参数 $w_i$ 对于优化函数的梯度： $g_{t}=\ abla f(w)$
更新参数： $w_{t}=w_{t-1}-\\alpha \\cdot g_{t}$ 。其中 $\\alpha$ 是学习率

更多的后面的优化算法其实将上述步骤2中的 $g_{t}$ 变得更加复杂，这里我们可以得到一个优化算法的重要框架：

Step 1: 计算参数关于优化函数的基本梯度 $g_{t}=\ abla f(w)$

Step 2: 计算用于更新参数的下降梯度 $\\eta_t=\\phi(g_1, g_2, ..., g_t)$

Step 3: 更新参数 $w_{t}=w_{t-1}-\\alpha \\cdot \\eta_{t}$

接下来，分析新的优化器都我们都可以按照这三步分析。

显然SGD是 $\\eta_t=g_t$ 的情况，所以也是最简单的优化器。它的缺点也很多，收敛速度很慢，因为在local optima附近梯度较小所以容易陷入其中，振荡情况也很明显。

SGD有一点很不好，它每一次优化算得的 $\\eta_t$ 都是由当前时刻的梯度决定的，在一个优化函数中，如果在到达全局最优点时函数大体是下降的趋势，我们希望优化器”记住“这个大体下降的趋势，而不是因为某个地方梯度小了些，就拒绝优化了。不妨想想石头从山上滚下的过程，它不会因为山上某个坑就不往下了，而是借助之前下落获得的冲量越过这个局部最小值，向全局最小值冲去。所以，我们给朴素的SGD引入了动量(momentum)这个概念，帮我们完成这项任务

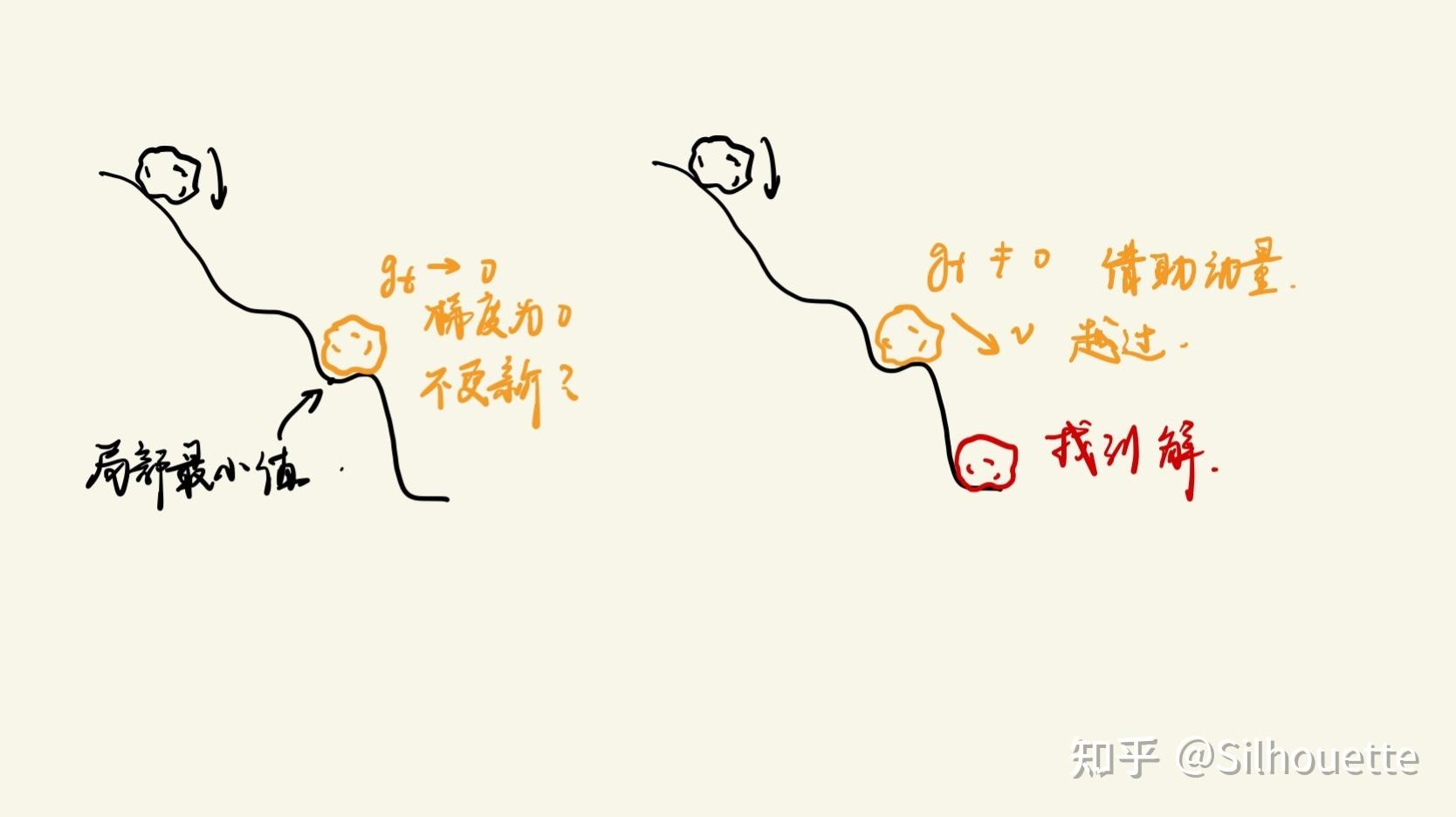
回想自己在PyTorch中定义优化器的时候，有一个参数就是momentum，即为动量

SGD with momentum原理如下：

Step 1: 计算参数关于优化函数的基本梯度 $g_{t}=\ abla f(w)$

Step 2: 计算动量 $m_t=\\beta_1 \\cdot m_{t-1}+ (1-\\beta_1) \\cdot g_t$ ；此时下降梯度 $\\eta_t=m_t$

Step3: 更新参数 $w_{t}=w_{t-1}-\\alpha \\cdot \\eta_{t}$

通常情况下， $\\beta_1=0.9$ ,意味着动量（惯性）占更新梯度的绝大部分，当前点的梯度值反而没那么重要了。

还是回到石头下坡的问题，一味地服从已知的梯度（表征过去梯度的动量 $m_t$ 和现在的基本梯度 $g_t$ ）也并不一定令人满意。我们更希望，在这个地方小球还能知道它下一个位置的梯度（预测梯度），从而采取更合理的优化方式，NAG就是基于这种思想提出来的。

Step 1: 计算参数关于优化函数的预测梯度 $\ ilde g_{t}=\ abla f(w-\\beta_1 \\cdot m_{t-1})$

Step 2: 计算动量 $m_t=\\beta_1 \\cdot m_{t-1}+ (1-\\beta_1) \\cdot \ ilde g_t$ ；此时下降梯度 $\\eta_t=m_t$

Step3: 更新参数 $w_{t}=w_{t-1}-\\alpha \\cdot \\eta_{t}$

之前介绍的方法，对于所有参数，都是按照同一个学习率更新的，但实际训练中，模型的权重和出现的特征（feature maps, embeddings etc.）是相互关联的。我们希望和高频特征关联的权重更新速率低（保证稳定），和低频特征关联的权重更新速率高（快速收敛）。一个例子便是NLP中的word embedding，遇到低频词语，模型需要较高的更新速率，反之对高频词语更新速率就要低。

既然AdaGrad能够使得每个参数获得不同的学习率，我们首先考虑对每个参数 $w_i$ 是如何更新的。

假设待优化参数为 ${w_1, w_2, ..., w_d}$ ，对于其中一个参数 $w_i$ ，它基本梯度是 $g_{t,i}$ ，即优化函数对 $w_i$ 的偏导数。

学习率则有变化，变成 $\\alpha_{t,i}=\\frac{\\alpha}{\\sqrt{\\sum_{\ au=1}^{t}{g_{\ au,i}^2}+\\epsilon}}$ ，其中求和的项是这个参数历史梯度的平方和， $\\epsilon$ 是一个平滑参数，实验表明，没有这项参数AdaGrad的效果会大大折扣。

由于此算法没有采用动量，故下降梯度 $\\eta_{t,i}=g_{t,i}$

所以最终表达式为 $w_{t,i}=w_{t-1,i}- \\alpha_{t,i}\\cdot \\eta_{t,i}$

最后，我们进行向量化(vectorize)的操作，将原来单个参数历梯度的平方和推广为所有参数，是一个对角矩阵

$G_t=[v_{t,1},v_{t,2}, ..., v_{t,d}]\ imes I_{d\ imes d}$ ，其中仍有 $v_{t,i}=\\sum_{\ au=1}^{t}{g_{\ au,i}^2}$ 。新的学习率向量为 $\\alpha_t=\\frac{\\alpha}{\\sqrt{G_t+\\epsilon}}$

综上所述，AdaGrad的流程表示为：

Step 1: 计算参数关于优化函数的基本梯度 $g_{t}=\ abla f(w)$

Step 2: 计算下降梯度时下降梯度 $\\eta_t=g_t$

Step3: 更新参数 $w_{t}=w_{t-1}-\\frac{\\alpha}{\\sqrt{G_t+\\epsilon}}\\odot \\eta_{t}$

AdaGrad使得优化器不用刻意控制学习率的变化，因而称为”自适应学习率“优化器，但由于学习率表达式的分母是单调递增的，所以学习率随着训练的进行会不断下降，从而导致模型的学习可能没法进行下去。

Adadelta和RMSprop为了解决上述AdaGrad提到的问题几乎是同时提出的，这里就放到一起讲。

RMSprop的 $v_i$ 只计算过去某个时间 $t_{start}=t - k$ 开始k个步长以内的梯度平方和，而不是从 $t=1$ 开始计算，同时有一个参数 $\\gamma$ ，将原来的平方和改写成加权平方和。

$G_t=\\beta_2 \\cdot G_{t-1}+ (1-\\beta_2) \\cdot g_t^2$

Step 1: 计算参数关于优化函数的基本梯度 $g_{t}=\ abla f(w)$

Step 2: 计算下降梯度时下降梯度 $\\eta_t=g_t$

Step3: 更新参数 $w_{t}=w_{t-1}-\\frac{\\alpha}{\\sqrt{G_t+\\epsilon}}\\odot \\eta_{t}$

为了后续表示方便，我们就将 $\\sqrt{G_t+\\epsilon}$ 记为 $RMS[g]_t$ （root mean square）

再讲AdaGrad。Adadelta思路和RMSprop相像，但它的参数更新方式和梯度更新有一点区别，它的参数更新是逐步”累加“得到，形如：

$w_t=w_{t-1}+ \\Delta w_t$

而 $\\Delta w_t$ 的计算方式如下（计算方式有点套娃那味儿）：

我们把上述RMS的参数由梯度换成我们要计算的 $\\Delta w_t$ ，即 $RMS[\\Delta w_t]=\\sqrt{W_t+\\epsilon}$ ， $W_t$ 就是过去一个时间窗口内的 $\\Delta w_t$ 的加权平方和，

最终的 $\\Delta w_t$ 计算方式为： $\\Delta w_t=-\\frac{RMS[\\Delta w]_{t-1}}{RMS[g]_t}\\cdot g_t$

总是，计算这个RMS就是存储下之前k个时间点计算的 $g_t$ 和 $\\Delta w$ ，然后套加权平方和公式就行啦。

Adam 其实就是将上述算法综合，既有Adaptive，也有动量，可以看做是RMSprop和SGD with momentum的结合 $m_t=\\beta_1 \\cdot m_{t-1}+ (1-\\beta_1) \\cdot g_t$ ， $G_t=\\beta_2 \\cdot G_{t-1}+ (1-\\beta_2) \\cdot g_t^2$

由于 $m_t, G_t$ 的初始值均为0-vector, 一开始它们不容易更新起来，因此加入bias-correction计算：